
Path-Inference-Filter(PIF) 算法调用的实现
Path Inference Filter(PIF, 道路推断滤波)算法是一种基于概率的路网匹配算法。其核心代码已经开源在 GitHub 上,作者也提供了一个example.py文件,来介绍如何使用。我由于需要将此算法真实用于路网匹配中,因此需要根据实际路网对此算法进行调用。之前使用 ArcPy 写了一个,但是运行速度非常慢,而且跑着跑着电脑就自动关机了。所以现在就用 PostGIS 和 pgRouting 重新实现一个版本。
PIF 的数学原理
此处详细情况请参考论文 The Path Inference Filter: Model-Based Low-Latency Map Matching of Probe Vehicle Data 。后面我会补充一个自己整理的简略版原理。
PIF 的接口调用
PIF 核心库提供了一些类供我们使用。比如:
State和StateCollection:描述状态值的类及状态值的集合。LatLng:表示经纬度的对象。PathBuilder:路径建立类。用于生成状态值之间的可达路径。LearningTrajectory:用于获取轨迹的描述。TrajectoryViterbi1:用于计算概率最大的轨迹。TrajectorySmoother1:用于滤波。
State、StateCollection、LatLng三个类可以直接使用。对于我们拿到的 GPS 数据来说,一般都会有一些附加的属性值,例如速度、方向、车辆状态等。可以创建自己的继承自LatLng和State的子类,添加这些属性。
我们可以将一些常用的函数,封装到类WuhanRoadFilter中,例如:计算距离的函数distance、计算状态值特征向量和路径特征向量的函数等。该类的形式如下:
1 | class WuhanRoadFilter: |
在调用过程中,可以创建PathBuilder的子类,来实现自己的路径搜索。子类中只需要实现方法getPaths()。此方法用于在方法getPathsBetweenCollections()中调用以获取路径。必须实现,否则会抛出NotImplementedError的错误。我们创建类WuhanRoadBuilder,在该类中实现getPaths()方法。该类的形式如下:
1 | class WuhanRoadBuilder(PathBuilder): |
这些函数和 PIF 框架的调用过程可参考 PIF 库中的example.py文件。
利用 pgRouting 实现调用 PIF 算法
借助 PostGIS 和 pgRouting 可以实现路径搜索功能,而使用 PostGIS 提供的大量的关于几何和地理数据的函数,可以方便实现对 PIF 算法的调用。但是这里需要编写的数据库函数,需要一定的数据库编程的能力。为了能够和 Python 编写的 PIF 核心代码结合起来,需要使用 Python 调用 PostgreSQL 函数,并将结果转化为 Geometry 及其子类型的对象。
使用到的 Python 包
使用下面两个包即可:
准备路网数据
假设我们要导入的路网数据名字叫road。一般情况下,我们拿到的数据,坐标系为 WGS84 或常用的投影坐标系(如CGCS2000)。在 WGS84 坐标系下的数据,以Geography类型存储在数据库中,在投影坐标系下的数据,以Geometry类型存储在数据库中。在 PostGIS 的文档中,建议使用Geometry类型存储数据,以减小计算量。
The geography type allows you to store data in longitude/latitude coordinates, but at a cost: there are fewer functions defined on GEOGRAPHY than there are on GEOMETRY; those functions that are defined take more CPU time to execute.
Geography 类型允许你以经纬度坐标的方式存储数据,但是代价是:Geography 类型比 Geometry 类型的函数少;Geography 类型的函数执行起来消耗更多的 CPU 时间。
The type you choose should be conditioned on the expected working area of the application you are building. Will your data span the globe or a large continental area, or is it local to a state, county or municipality?
- If your data is contained in a small area, you might find that choosing an appropriate projection and using GEOMETRY is the best solution, in terms of performance and functionality available.
- If your data is global or covers a continental region, you may find that GEOGRAPHY allows you to build a system without having to worry about projection details. You store your data in longitude/latitude, and use the functions that have been defined on GEOGRAPHY.
- If you don’t understand projections, and you don’t want to learn about them, and you’re prepared to accept the limitations in functionality available in GEOGRAPHY, then it might be easier for you to use GEOGRAPHY than GEOMETRY. Simply load your data up as longitude/latitude and go from there.
因此,我们采用投影坐标系的路网数据。
数据导入
导入时数据的方法非常简单,使用 PostGIS Shapefiel Import/Export Manager(PostGIS 2.0 Shapefile and DBF Loader Exporter) 工具导入即可。
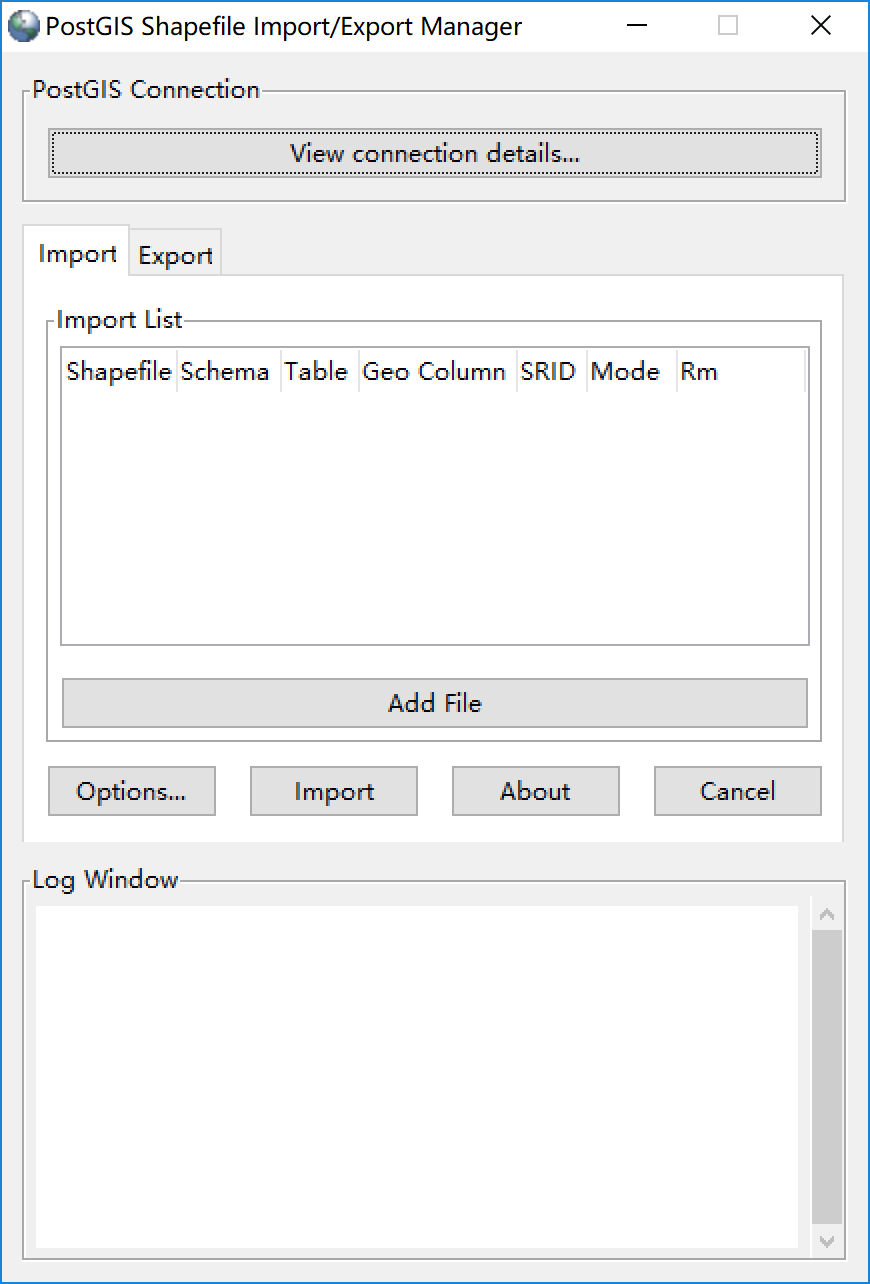
在这个工具上设置数据库的连接,选择要导入的 shp 文件。选定 shp 文件后,最好点击 Options 按钮打开选项,选中最后一个复选框。
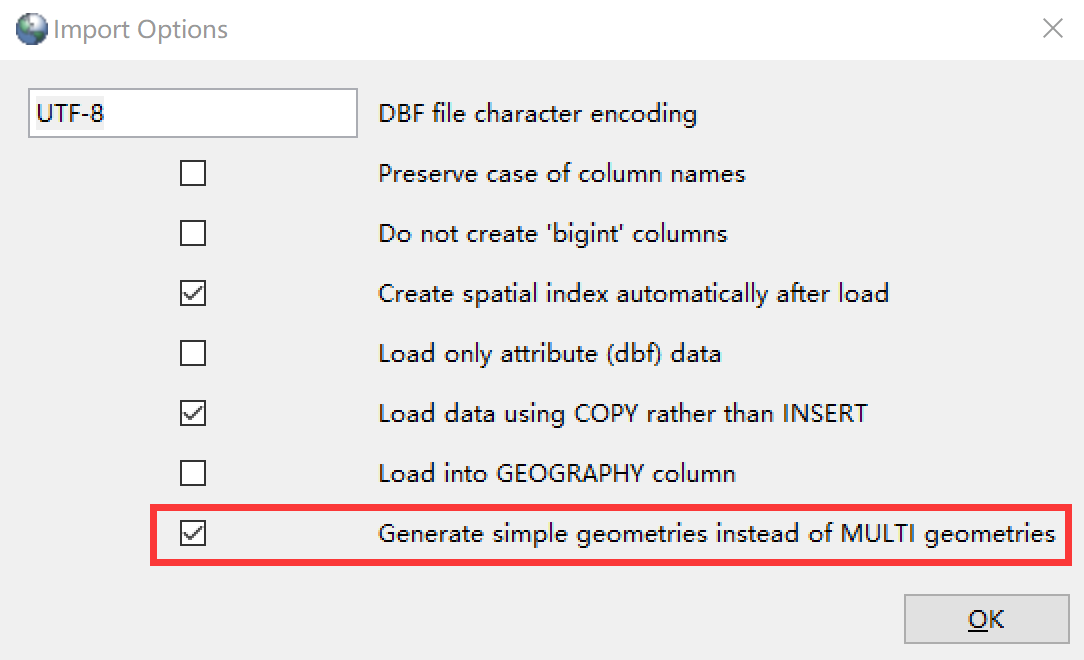
确定后,点击 Improt 按钮开始导入。等待其完成即可。
需要注意的是,shp 文件的名字,会作为最终导入到数据库中表的名字。
拓扑关系建立
我们导入的数据集,在网络结构中数据“边”类型,pgRouting 称之为 edge。pgRouting 需要知道每个 edge 的起点和终点的序号是什么,需要知道路径的长度是多少。需要给road数据集添加三个字段:source、target和length:
1 | ALTER TABLE road ADD COLUMN source integer; |
当然这两个字段的名字可以自己取。路径长度字段如果已经有了,也可以不用重新建立。
然后是拓扑关系的建立。使用 pgRouting 提供的函数 pgr_createTopology() 来创建拓扑,该函数有以下参数:
| 参数名 | 说明 |
|---|---|
edge_table | 路网表名(也可以包含数据库名)。文本类型。 |
tolerance | 路段不连续误差。8字节浮点数类型。 |
the_geom | 路网表中 Geometry 列的名称(默认是”the_geom”)。文本类型。 |
id | 路网表中主键列的名称(默认是”id”)。文本类型。 |
source | 路网表中 source 列的名称(默认是”source”)。文本类型。 |
target | 路网表中 target 列的名称(默认是”target”)。文本类型。 |
rows_where | 用于选择一个子集或多行的 SELECT 条件。默认值是选择所有 source 和 target 为空的行。文本类型。 |
clean | 是否清除之前的拓扑关系(默认是 false )。布尔型。 |
具体调用实例为:
1 | SELECT pgr_createTopology('public.road', 0.001, 'geom', 'gid'); |
路网数据准备完成。
计算两点间距离
这里只需要使用到 PostGIS 提供的函数ST_Distance(),函数的用法非常简单,可参考官网文档。为了方便调用,我们设计一个数据库函数PIF_GetDistance(),使其可以直接输入两个坐标值,进行距离计算。
1 | CREATE OR REPLACE FUNCTION "public"."PIF_GetDistance"("x1" float8, "y1" float8, "x2" float8, "y2" float8) |
Python 中调用此函数:
1 | def distance(self, coord1: LatLng, coord2: LatLng) -> float: |
获取每个 GPS 点对应的状态值
状态值的获取是在一个路段上计算一个联合分布 $$ π(x|g) = ω(g|x)Ω(x) $$ 其中 $ x $ 是状态值,$ g $ 是 GPS 观测值。但是由于分布 $ ω(g|x) $ 服从正态分布,$ Ω(x) $ 在没有先验知识的情况下,服从均匀分布,因此直接取路段上距离 GPS 观测值最近的点即可。
需要使用到的 PostGIS 函数
编写这个数据库函数,需要用到 PostGIS 提供的一些函数,如下(参考 PostGIS 文档):
| 函数 | 用途 |
|---|---|
ST_Point(float, float) | 构造 Point 对象的函数。 |
ST_SetSRID(geometry, integer) | 设置对象的 SRID(即空间参考)。 |
ST_Transform(geometry, integer) | 将 Geometry 对象进行投影转换。 |
ST_StartPoint(geometry) | LineString Geometry 对象的第一个点。 |
ST_EndPoint(geometry) | LineString Geometry 对象的最后一个点。 |
ST_ClosestPoint(geometry, geometry) | 返回第一个 Geometry 对象上距离第二个 Geometry 对象最近的点。 |
ST_LineLocatePoint(geometry a_linestring, geometry a_point) | 返回a_line上距离a_point最近的点在a_line上的百分比。 |
编写 PostgreSQL 函数
函数实现的思路是:首先按照范围筛选处距离指定 GPS 观测值一定距离(例如 100 m)内的路段,然后在这些路段上计算每个最近点。
数据库函数PIF_GetStatesAtPosition()的定义如下:
1 | CREATE OR REPLACE FUNCTION public.pif_GetStatesAtPosition( |
为了避免投影误差,可以将所有结果中的坐标直接以 EPSJ:3857 坐标返回,下次调用时直接用这个坐标系的坐标。这样做同时也可以减少计算量。
Python 函数的编写
使用 Python 调用这个函数时,直接使用 psycopg2 包查询该函数即可。对于返回结果进行处理,分别创建State对象,最后添加到StateCollection对象中,并返回。
1 | def get_posibility_states(self, point: TaxiPoint, distance: float): |
这种查询的方法同样适合于其他支持空间数据的数据库,以及其他类型的语言,例如 C# 和 Java 语言,数据库也可以换成 SQL Server 等其他数据库。问题在于,几乎运行前期绝大部分计算任务都在数据库中完成,数据库计算的压力会比较大,选择一个合适的数据库非常重要。
获取状态值间的最短路径
根据 PIF 算法的原理,将 GPS 点映射至 $ I^t $ 个元素的候选状态集合 $ \mathbf{x}^t = {x_1^t, x_2^t, ⋯, x_{I^t}^t} $ ,再映射至 $ J^t $ 个元素的路经集合。即对于 $ ∀x_i^t ∈ x^t, \mathbf{x}_i^{t+1} \in \mathbf{x}^{t+1} $,都构造一条路径。路径集记为 $ \mathbf{p}^t $,轨迹为:$$ τ = x_1p_1x_2⋯p_{t-1}x_t $$ PIF 会根据车辆轨迹计算概率,最终取概率最高的一条轨迹作为出租车 GPS 序列再地图上匹配得到的轨迹。
数据库函数的编写
PostgreSQL 数据库的插件 pgRouting 提供了路径规划的能力。在建立拓扑关系后,可以使用路径规划系列函数求解最短路径。
pgr_dijkstra():使用 Dijkstra 算法求解的最短路径。除此之外,还有求解代价的 Dijkstra 函数。pgr_aStar():使用 A* 算法求解最短路径。该系列函数即将不受官方支持。
以pgr_dijkstra()为例,它的参数有:
| 参数名 | 类型 | 说明 |
|---|---|---|
sql | 文本 | 一个 SQL 查询。 |
source | int4 | 起点的 ID。 |
target | int4 | 终点的 ID。 |
directed | boolean | 如果地图是有向的,那么为ture。 |
has_rcost | boolean | 如果为true,SQL 查询的reverse_cost会被用来计算代价值。 |
其中 SQL 查询形如
1 | SELECT id, source, target, cost [,reverse_cost] FROM edge_table |
返回列有:
| 列名 | 类型 | 说明 |
|---|---|---|
id | int4 | 边的 ID。 |
source | int4 | 起点的 ID。 |
target | int4 | 终点的 ID。 |
cost | float | 边的代价值。为负则不考虑此边 |
reverse_cost | 可选 | 边的往返代价值。只在directed和has_rcost参数为true时使用。 |
但是 pgRouting 提供的函数,只支持从路网数据的一个节点到另一个节点,也就是不支持任意两点间的最短路径。我们需要自己撰写函数来实现这一点。对于两个点 $ p_1,p_2 $,求解其间最短路径 $ p_1p_2$ 实现的思路如下:
- 找到 $ p_1,p_2 $ 最近的线段 $ l_1, l_2$
- 找到 $ l_1 $ 的终点 $p_t$(即
target值),和 $ l_2 $ 的起点 $p_s$(即source值)。 - 求解从
target到source的最短路径 $ p $。 - 将 $ p $ 补上或删除 $ p_1p_t $ 和 $ p_sp_2 $ 两段。
由于在 PIF 中, 要求解路径的点是两个状态值,都在路网上,因此,在搜索最近路段时,搜索范围可放小一点,如 1 m。
根据博客,具体函数实现如下(做了一些修改):
1 | CREATE OR REPLACE FUNCTION "public"."pif_getpathbetweenpoints"("startx" float8, "starty" float8, "endx" float8, "endy" float8) |
修改的地方:
- 固定了要查询的表。
- 将结果转换为 WGS84 坐标系。
- 在返回路径的同时返回了整个路径的长度。
Python 调用函数的编写
与之前类似,Python 调用函数的实现如下:
1 | def getPaths(self, s1: State, s2: State): |
路径结果后处理
在 PIF 核心库中,对两个车辆状态 $ x_i^{t} \in \mathbf{x}^{t} ,x_j^{t+1} \in \mathbf{x}^{t+1} $ 中间的路径 $ p_i $ 有要求。即 $ x_i^{t} $ 所在的路段的 ID 和 $x_j^{t+1}$ 所在路段的 ID 分别和 $ p_i $ 第一个路段的 ID 和 最后一个路段的 ID 相同。在不直接使用路段的 ID 作为最短路径搜索的返回值时,我们需要做一些处理。
产生这个问题原因,是 PIF 库的示例代码中,采用 $ ((x_S, y_S), (x_T, y_T)) $ 来表示 $ x_i^{t} $ 所在的路段 ID。若记获取某个状态值所在路段的 ID 的函数是 $ \mathbf{id}(x) $,则要求 $ \mathbf{id}(x_i^{t}) = \overrightarrow{ST} = (p_i)_1 $,$ S, T $ 是路段的起点和终点。同理,$ \mathbf{id}(x_i^{t}) = \overrightarrow{ST} = (p_i)_{-1} $($(p_i)_{-1}$ 表示最后一个搜索到的路径的最后一个路段)。
对于起始状态,理论上共有 6 种可能。如下图所示。记起始状态点为 $X$,其可能的 6 种情况分别为 $ \left\lbrace x_1, x_2, \cdots, x_6 \right\rbrace $,其所在路段 $ \mathbf{l} = \overrightarrow{ST}$ 起点为 $S$,终点为 $T$,匹配到的整个路径为 $ P $。记符号 $ \lnot \mathbf{L} = \overrightarrow{TS} $。
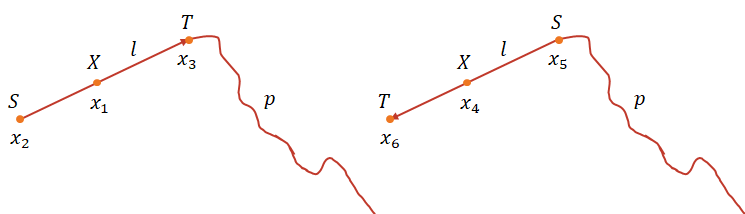
对于每个 $ X \in \left\lbrace x_1, x_2, \cdots, x_6 \right\rbrace $
- $ X = x_1 \neq S \neq T \wedge T = P_2 $ :这是最一般的情况。只需令 $ P = \left\lbrace S \right \rbrace \cup P $ 即可。
- $ X = S \wedge T = P_2 $ :此种情况无需处理。
- $ X = T \wedge S \neq P_2 $ :令 $ P = \left\lbrace S \right \rbrace \cup P $。
- $ X = x_1 \neq S \neq T \wedge S = P_2 $ :令 $ \mathbf{id}(X) = \lnot \mathbf{l} $。
- $ X = S \wedge T \neq P_2 $ :令 $ P = \left\lbrace T \right \rbrace \cup P $,且 $ \mathbf{id}(X) = \lnot \mathbf{l} $。
- $ X = T \wedge S = P_2 $ :令 $ \mathbf{id}(X) = \lnot \mathbf{l} $。
对于结束状态,可能的情况如下图。
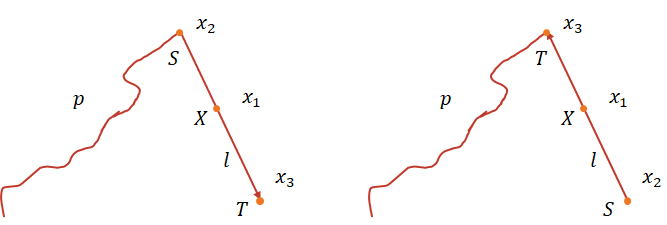
处理方法可与上同理。
由于 pgRouting 的问题,好像会给求得的路径按照坐标大小排个序?我目前遇到过一次,因此,在进行上述处理之前,判断一下,起始状态和结束状态的坐标值是不是分别和路径的第一个点和最后一个点相同,如果不是,把路径反过来。
在理论上,上述 6 种情况是合理的。但是在实际运行过程中,竟然产生了 $$ X = x_1 \neq S \neq T \wedge T = P_2 \wedge S = P_2 $$ 的情况,因此还需要做一个处理。如果上述 6 种情况都不满足,视为没找到路径。