A Hierarchical and Geographically Weighted Regression Model and Its Backfitting Maximum Likelihood Estimator

Author

Yigong Hu

Published

March 25, 2023

Hierarchical and geographically weighted regression (HGWR) is a spatial modelling method designed for data with a spatially hierarchical structure, i.e., samples are grouped by their locations. Variables are divied into group level and sample level. It calibrate three types of effects: local fixed effects, global fixed effects, and random effects. Only group level variables can be local fixed effects. In this post, the usage and some examples are going to be shown with R code.

Installation

The HGWR model is implemented with C++ and R codes. And we have published an R package hgwrr to provice easy-to-use user interfaces to build HGWR moddels.

From CRAN

Install the hgwrr package from CRAN is very easy, through

install.packages("hgwrr")

Note if you are using Linux or macOS platforms, this package requires GSL to be installed and can be found by R. Please install it using your package manager, like apt, dnf, and brew. On Windows, the pre-built binary package would be provided by CRAN.

From Source Code

Please download the [R source package (v0.3.0)] and install it via the following code

R CMD INSTALL hgwrr_0.3-0.tar.gz

Please make sure that the following dependencies are already installed in your R environment:

  • Armadillo
  • GSL

Just the package-manager versions are enough.

Usage

An HGWR model can be calibrated using the following function,

hgwr(
  formula, data, local.fixed, coords, bw,
  alpha = 0.01, eps_iter = 1e-06, eps_gradient = 1e-06, max_iters = 1e+06,
  max_retries = 1e+06, ml_type = HGWR_ML_TYPE_D_ONLY, verbose = 0
)

There seems to be quite a few arguments, but most of them have default values which would be fine on most ocassions. The first five arguments are mandatory.

formula

This argument accepts a formula object in R. Its format follows lme4 package. As there are two types of effects: fixed effects and random effects, we use the following format to specify both of them

dependent ~ fixed1 + fixed2 + (random1 + random2 | group)
data
It accepts a DataFrame object in R. All variables specified in formula are extracted from data. In this stage, Spatial*DataFrame is not supported, and will not be supported in the future.
local.fixed
It accepts a list of character specifying which fixed effects are local. For example, if fixed1 needs to be locally fixed, then set local.fixed to c("fixed1").
coords
It accepts a matrix of 2 columns. Each row is the longitude and latitude of each group.
bw
It accepts an integer or numeric number to specify the bandwidth used in geographically weighted process. Currently, it can only be adaptive bandwidth.

For other arguments, if the default values cause some problems, and you want to change some of them, please check the documentation of function hgwr() for more infomation.

Simulation Experiment

To carry out the experiment, there are some packages required to be in your R environment. Please install them if they are abscent.

The CRAN versions now are fine.

library(tidyverse)
library(ggpubr)
library(Metrics)
library(sf)
library(hgwrr)
library(GWmodel)
library(lmerTest)

Data Generation

The data used in this experiment is generated by the following code. This process is inspired by Fotheringham, Yang, and Kang (2017).

nu <- 25
nv <- 25
ncoords <- nu * nv
coords <- matrix(c(rep(seq_len(nu) - 1, each = 25), rep(seq_len(nv) - 1, times = 25)), ncol = 2) %>% as.data.frame()
colnames(coords) <- c("u", "v")
u <- coords[["u"]]
v <- coords[["v"]]
g1 <- (36 - (6 - u/2)^2)*(36 - (6 - v/2)^2)/324
g2 <- 4 * exp(- (scale(u)^2 + scale(v)^2)/2)
h1 <- rep(2, times = ncoords)
set.seed(648)
z1 <- rnorm(ncoords, mean = 2, sd = 0.5)
set.seed(12574)
b0 <- (u + v) / 12 - 2 + rnorm(ncoords, mean = 2, sd = 0.2)
betas <- data.frame(Intercept = b0, g1, g2, h1, z1)
set.seed(648)
nsamples <- floor(runif(ncoords, 20, 50))
iloc <- rep(seq_len(ncoords), times = nsamples)
set.seed(1)
x <- MASS::mvrnorm(sum(nsamples), mu = rep(0, 4), Sigma = diag(4))
x[,1] <- aggregate(x[,1], by = list(iloc), FUN = mean)[["x"]] %>% rep(times = nsamples)
x[,2] <- aggregate(x[,2], by = list(iloc), FUN = mean)[["x"]] %>% rep(times = nsamples)
colnames(x) <- c("g1", "g2", "h1", "z1")
set.seed(2)
e <- rnorm(sum(nsamples))
y <- rowSums(cbind(1, x) * as.matrix(betas[iloc,])) + e
data <- cbind(y = y, x, group = iloc) %>% as.data.frame()
sim <- list(
    data = data,
    betas = betas,
    coords = coords
)
sim_sf <- st_as_sf(with(sim, cbind(data, coords[data$group,])), coords = c("u", "v"))
glimpse(sim)
List of 3
 $ data  :'data.frame': 21434 obs. of  6 variables:
  ..$ y    : num [1:21434] 4.274 0.952 -2.278 1.21 4.547 ...
  ..$ g1   : num [1:21434] -0.154 -0.154 -0.154 -0.154 -0.154 ...
  ..$ g2   : num [1:21434] 0.109 0.109 0.109 0.109 0.109 ...
  ..$ h1   : num [1:21434] 3.169 -0.031 -1.092 -0.983 1.719 ...
  ..$ z1   : num [1:21434] -0.626 0.184 -0.836 1.595 0.33 ...
  ..$ group: num [1:21434] 1 1 1 1 1 1 1 1 1 1 ...
 $ betas :'data.frame': 625 obs. of  5 variables:
  ..$ Intercept: num [1:625] 0.35 0.429 0.33 0.267 0.465 ...
  ..$ g1       : num [1:625] 0 0 0 0 0 0 0 0 0 0 ...
  ..$ g2       : num [1:625] 0.252 0.314 0.384 0.461 0.543 ...
  ..$ h1       : num [1:625] 2 2 2 2 2 2 2 2 2 2 ...
  ..$ z1       : num [1:625] 2.46 2.63 1.25 1.91 1.91 ...
 $ coords:'data.frame': 625 obs. of  2 variables:
  ..$ u: num [1:625] 0 0 0 0 0 0 0 0 0 0 ...
  ..$ v: num [1:625] 0 1 2 3 4 5 6 7 8 9 ...

With this data, we are going to calibrate a HGWR model, geographically weighted regression (GWR, Brunsdon, Fotheringham, and Charlton 1996) model, multiscale geographically weighted regression (MGWR, the PSDM implementation, Lu et al. 2017) model, and hierarchical linear model (HLM, Raudenbush 1993). The MGWR model requires a very large amout of memory and time, so we only demonstrate the workable codes here. The result we got on a high-performance computing platform is used instead.

Model Calibration

HGWR

A HGWR model is calibrated with the following code.

hgwr_formula <- y ~ g1 + g2 + h1 + (z1 | group)
hgwr_model <- hgwr(
    hgwr_formula, sim$data, c("g1", "g2"), sim$coords, "CV", 
    kernel = "bisquared",
)
summary(hgwr_model)
Hierarchical and geographically weighted regression model
=========================================================
Formula: hgwr_formula
 Method: Back-fitting and Maximum likelihood
   Data: sim$data

Diagnostics
-----------
 Rsquared 
 0.908050 

Scaled residuals
----------------
       Min         1Q    Median        3Q       Max 
 -3.995269  -0.648274  0.000561  0.652537  3.530948 

Other Information
-----------------
Number of Obs: 21434
       Groups: group , 625

GWR

sim_sp <- as(sim_sf, Class = "Spatial")
gwr_formula <- y ~ g1 + g2 + h1 + z1
gwr_bw <- bw.gwr(gwr_formula, sim_sp, approach = "AIC", adaptive = T, kernel = "bisquare")
Take a cup of tea and have a break, it will take a few minutes.
          -----A kind suggestion from GWmodel development group
Adaptive bandwidth (number of nearest neighbours): 13254 AICc value: 68302.68 
Adaptive bandwidth (number of nearest neighbours): 8199 AICc value: 67235.53 
Adaptive bandwidth (number of nearest neighbours): 5074 AICc value: 66677.95 
Adaptive bandwidth (number of nearest neighbours): 3143 AICc value: 66381.08 
Adaptive bandwidth (number of nearest neighbours): 1949 AICc value: 66152.06 
Adaptive bandwidth (number of nearest neighbours): 1212 AICc value: 65879.63 
Adaptive bandwidth (number of nearest neighbours): 755 AICc value: 65553.06 
Adaptive bandwidth (number of nearest neighbours): 474 AICc value: 65089.52 
Adaptive bandwidth (number of nearest neighbours): 299 AICc value: 64121.17 
Adaptive bandwidth (number of nearest neighbours): 192 AICc value: 113016 
Adaptive bandwidth (number of nearest neighbours): 366 AICc value: 64842.55 
Adaptive bandwidth (number of nearest neighbours): 258 AICc value: 63736.27 
Adaptive bandwidth (number of nearest neighbours): 232 AICc value: 63688.32 
Adaptive bandwidth (number of nearest neighbours): 216 AICc value: 64235.33 
Adaptive bandwidth (number of nearest neighbours): 241 AICc value: 63684.82 
Adaptive bandwidth (number of nearest neighbours): 248 AICc value: 63701.3 
Adaptive bandwidth (number of nearest neighbours): 238 AICc value: 63682.91 
Adaptive bandwidth (number of nearest neighbours): 235 AICc value: 63681.33 
Adaptive bandwidth (number of nearest neighbours): 234 AICc value: 63681.33 
gwr_model <- gwr.basic(gwr_formula, sim_sp, bw = gwr_bw, adaptive = T, kernel = "bisquare")
gwr_model
   ***********************************************************************
   *                       Package   GWmodel                             *
   ***********************************************************************
   Program starts at: 2023-03-30 11:46:44 
   Call:
   gwr.basic(formula = gwr_formula, data = sim_sp, bw = gwr_bw, 
    kernel = "bisquare", adaptive = T)

   Dependent (y) variable:  y
   Independent variables:  g1 g2 h1 z1
   Number of data points: 21434
   ***********************************************************************
   *                    Results of Global Regression                     *
   ***********************************************************************

   Call:
    lm(formula = formula, data = data)

   Residuals:
    Min      1Q  Median      3Q     Max 
-5.6729 -0.9458 -0.0075  0.9499  5.3801 

   Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
   (Intercept) 2.002434   0.009684  206.78   <2e-16 ***
   g1          1.659038   0.057600   28.80   <2e-16 ***
   g2          1.791212   0.056544   31.68   <2e-16 ***
   h1          2.010065   0.009660  208.09   <2e-16 ***
   z1          2.042761   0.009661  211.44   <2e-16 ***

   ---Significance stars
   Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 
   Residual standard error: 1.417 on 21429 degrees of freedom
   Multiple R-squared: 0.8064
   Adjusted R-squared: 0.8064 
   F-statistic: 2.232e+04 on 4 and 21429 DF,  p-value: < 2.2e-16 
   ***Extra Diagnostic information
   Residual sum of squares: 43019.04
   Sigma(hat): 1.416769
   AIC:  75771.36
   AICc:  75771.37
   BIC:  54445.03
   ***********************************************************************
   *          Results of Geographically Weighted Regression              *
   ***********************************************************************

   *********************Model calibration information*********************
   Kernel function: bisquare 
   Adaptive bandwidth: 234 (number of nearest neighbours)
   Regression points: the same locations as observations are used.
   Distance metric: Euclidean distance metric is used.

   ****************Summary of GWR coefficient estimates:******************
                 Min.  1st Qu.   Median  3rd Qu.    Max.
   Intercept -0.36804  1.37847  1.98864  2.63158  3.8950
   g1        -5.46208  0.37769  1.59423  2.78590 11.7942
   g2        -5.90918  0.79411  1.74163  2.85702 13.1842
   h1         1.51922  1.94629  2.01310  2.07438  2.3601
   z1         1.14097  1.83026  2.01883  2.21836  2.8169
   ************************Diagnostic information*************************
   Number of data points: 21434 
   Effective number of parameters (2trace(S) - trace(S'S)): 1348.983 
   Effective degrees of freedom (n-2trace(S) + trace(S'S)): 20085.02 
   AICc (GWR book, Fotheringham, et al. 2002, p. 61, eq 2.33): 63681.33 
   AIC (GWR book, Fotheringham, et al. 2002,GWR p. 96, eq. 4.22): 62482 
   BIC (GWR book, Fotheringham, et al. 2002,GWR p. 61, eq. 2.34): 50756.14 
   Residual sum of squares: 22014.71 
   R-square value:  0.9009503 
   Adjusted R-square value:  0.8942974 

   ***********************************************************************
   Program stops at: 2023-03-30 11:47:26

HLM

hlm_model <- lmerTest::lmer(y ~ g1 + g2 + h1 + z1 + (z1 | group), sim$data)
summary(hlm_model)
performance::r2(hlm_model)
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: y ~ g1 + g2 + h1 + z1 + (z1 | group)
   Data: sim$data

REML criterion at convergence: 64443.4

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-3.9791 -0.6478  0.0011  0.6521  3.5484 

Random effects:
 Groups   Name        Variance Std.Dev. Corr
 group    (Intercept) 0.7750   0.8804       
          z1          0.2511   0.5011   0.01
 Residual             1.0087   1.0044       
Number of obs: 21434, groups:  group, 625

Fixed effects:
             Estimate Std. Error        df t value Pr(>|t|)    
(Intercept) 1.991e+00  3.595e-02 6.202e+02  55.377  < 2e-16 ***
g1          1.581e+00  2.093e-01 6.230e+02   7.552 1.53e-13 ***
g2          1.805e+00  1.988e-01 6.261e+02   9.079  < 2e-16 ***
h1          2.014e+00  7.043e-03 2.037e+04 286.022  < 2e-16 ***
z1          2.026e+00  2.136e-02 6.228e+02  94.830  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
   (Intr) g1     g2     h1    
g1  0.007                     
g2  0.021 -0.041              
h1  0.000 -0.001  0.000       
z1  0.007  0.001  0.000  0.002
# R2 for Mixed Models

  Conditional R2: 0.902
     Marginal R2: 0.803

MGWR

mgwr_model <- gwr.multiscale(y ~ g1 + g2 + h1 + z1, sim_sp, adaptive = T)
mgwr_model
   ***********************************************************************
   *                       Package   GWmodel                             *
   ***********************************************************************
   Program starts at: 2023-01-07 00:33:30 
   Call:
   gwr.multiscale(formula = y ~ g1 + g2 + h1 + z1, data = sim_sp, 
    adaptive = T, hatmatrix = F, parallel.method = "omp", parallel.arg = 48)

   Dependent (y) variable:  y
   Independent variables:  g1 g2 h1 z1
   Number of data points: 21434
   ***********************************************************************
   *                       Multiscale (PSDM) GWR                          *
   ***********************************************************************

   *********************Model calibration information*********************
   Kernel function: bisquare 
   Adaptive bandwidths for each coefficient(number of nearest neighbours): 
              (Intercept)    g1    g2    h1 z1
   Bandwidth          382  1054   474 19875 62

   ****************Summary of GWR coefficient estimates:******************
                  Min.   1st Qu.    Median   3rd Qu.   Max.
   Intercept  0.244383  1.451943  1.998243  2.611283 3.8138
   g1        -0.072043  0.746596  1.426176  2.567027 4.2021
   g2        -1.955412  0.969786  1.738936  2.659654 4.9470
   h1         2.003644  2.010011  2.015701  2.019937 2.0227
   z1         0.287334  1.691472  2.039915  2.376235 3.5291
   ************************Diagnostic information*************************

   ***********************************************************************
   Program stops at: 2023-01-07 04:58:17

Estimate Analysis

As the actual values of coefficients are already known, we can compare the performance of these models by comparing the closeness between their estimates and actual values.

Create some handy variables. 
coef_names <- c("Intercept", "g1", "g2", "h1", "z1")
coef_names_plot <- c("Intercept", "g1", "g2", "z1")
coef_name_map <- list(
    Intercept = "alpha[0]",
    g1 = "gamma[1]",
    g2 = "gamma[2]",
    h1 = "beta[1]",
    x1 = "beta[1]",
    z1 = "mu[1]"
)
coef_name_labels <- list(
    Intercept = bquote(alpha[0]),
    g1 = bquote(gamma[1]),
    g2 = bquote(gamma[2]),
    h1 = bquote(beta[1]),
    x1 = bquote(beta[1]),
    z1 = bquote(mu[1])
)
models_name <- c("GWR", "MGWR", "HLM", "HGWR")

Firstly, we collect coefficient estimates.

### Real values
beta0 <- sim$betas[coef_names]
### HGWR
hgwr_betas <- coef(hgwr_model)[coef_names]
### GWR
gwr_betas <- gwr_model$SDF@data[coef_names] %>%
    aggregate(by = list(sim$data$group), FUN = mean) %>%
    as.tibble() %>%
    select(all_of(coef_names))
Warning: `as.tibble()` was deprecated in tibble 2.0.0.
ℹ Please use `as_tibble()` instead.
ℹ The signature and semantics have changed, see `?as_tibble`.
### MGWR
mgwr_betas <- mgwr_model$SDF@data[coef_names] %>%
    aggregate(by = list(sim$data$group), FUN = mean) %>%
    as.tibble() %>%
    select(all_of(coef_names))
### HLM
hlm_betas <- coef(hlm_model)$group
colnames(hlm_betas)[1] <- "Intercept"
hlm_betas <- hlm_betas[coef_names]
models_coef <- map(models_name, ~ get(paste0(tolower(.x), "_betas")))
names(models_coef) <- models_name
models_coef_real <- c(list(Real = beta0), models_coef)

Then, plot estimate values at their location and the real values to see their distributions.

models_coef_real %>%
    map_dfr(function(x) {
        select(x, all_of(coef_names)) %>%
            map_dfr(~ data.frame(Value = .x, sim$coords), .id = "Coefficient")
    }, .id = "Algorithm") %>% 
    mutate(Algorithm = ordered(as.factor(Algorithm), names(models_coef_real)),
           Coefficient = ordered(as.factor(Coefficient), coef_names, 
                                 labels = coef_name_map[coef_names])) %>%
    ggplot(aes(u, v, fill = Value)) + geom_raster() + 
        scale_x_continuous(expand = expansion()) +
        scale_y_continuous(expand = expansion()) +
        scale_fill_gradient2(limits = c(0, 4), low = "#000099", 
                             mid = "#CCFF33", high = "#CC0033",
                             midpoint = 2, oob = scales::squish) +
        facet_grid(rows = vars(Algorithm), cols = vars(Coefficient), labeller = label_parsed) +
        coord_fixed() + theme_bw() +
        theme(legend.position = "bottom", legend.key.height = unit(10, "pt"))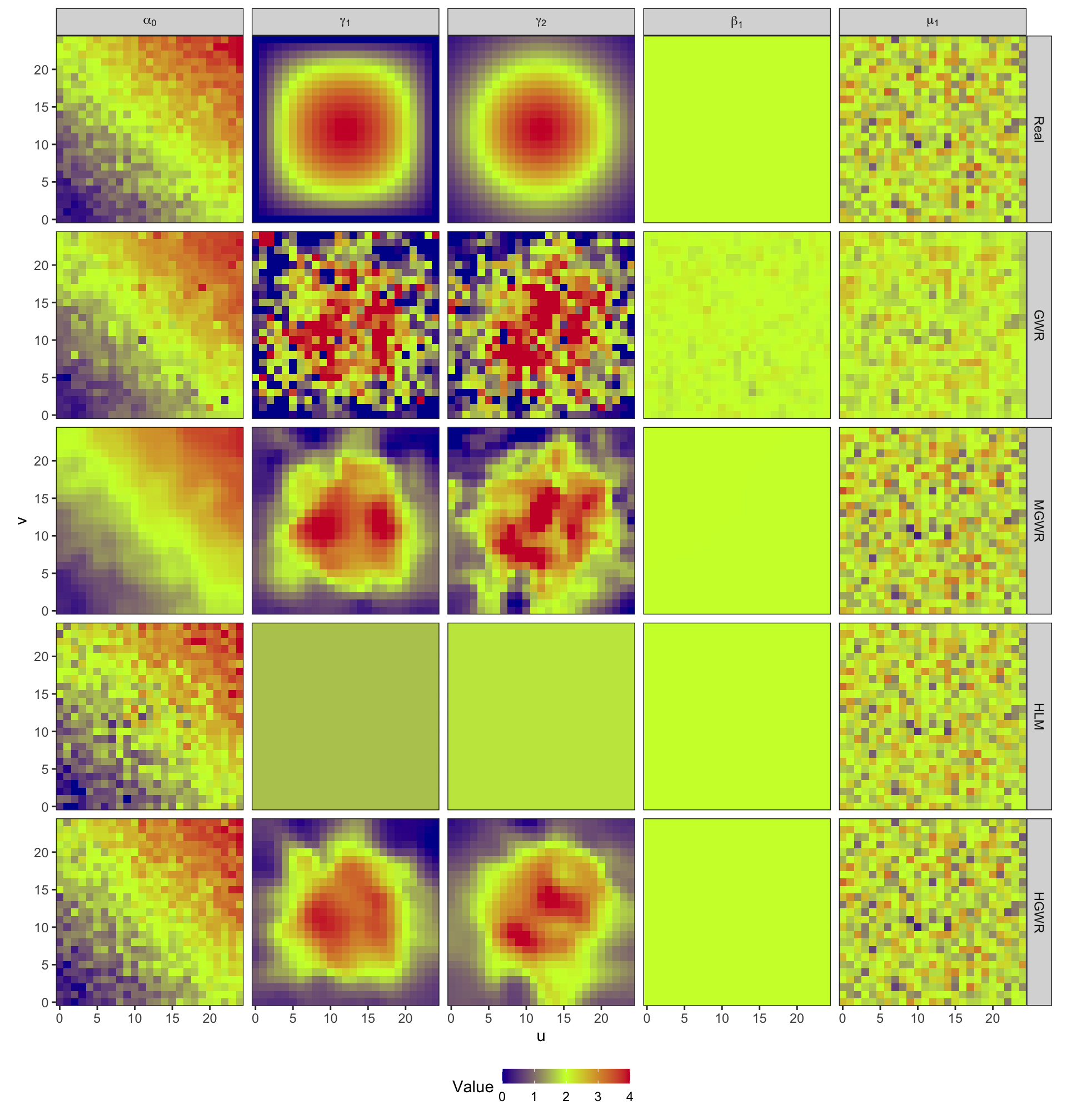

A scatter plot along with it may be useful.

beta_hat_real <- models_coef %>%
    map_dfr(function(x) {
        map_dfr(coef_names, ~ data.frame(Coefficient = .x, Estimated = x[[.x]], Real = beta0[[.x]]))
    }, .id = "Algorithm") %>%
    mutate(Algorithm = ordered(as.factor(Algorithm), names(models_coef)),
           Coefficient = ordered(as.factor(Coefficient), coef_names, labels = coef_name_map[coef_names]))
beta_hat_rmse <- beta_hat_real %>%
    group_nest(Algorithm, Coefficient) %>%
    mutate(rmse = map(data, ~ sqrt(mean((.x$Estimated - .x$Real)^2))),
           data = NULL)
ggplot(beta_hat_real, aes(x = Real, y = Estimated)) +
    geom_point() + geom_abline(intercept = 0, slope = 1) +
    geom_text(aes(x = -Inf, y = Inf, label = sprintf("RMSE=%.3f", rmse)),
              data = beta_hat_rmse, hjust = 0, vjust = 1.2) +
    scale_y_continuous(limits = c(-5, 10), oob = scales::squish) +
    facet_grid(rows = vars(Algorithm), cols = vars(Coefficient), labeller = label_parsed) +
    theme_bw()

From these two figures, we can find that:

  1. In the results of GWR, spatial heterogeneity is revealed in estimates for all variables. Although \(\hat{\beta}_1\) should be constant across the study area, GWR still generate spatially varying estimates for it. This is a kind of over-fitting from the spatial perspective. Besides, as the bandwidth is small, estimates for \(\gamma_1\) and \(\gamma_2\) are too local. Consequently, there are quite a few outliers disrupting the spatial trend.
  2. MGWR partly gets over issues of GWR by adopting parameter-specified bandwidths, instead of a uniform bandwidth. And it performs better when estimating \(\gamma_1\) and \(\gamma_2\). For global fixed effects, MGWR still generates spatially varying estimates, but they vary much slightly than estimates from GWR. For random effects, the results are slightly smoothed as well. MGWR also borrow a few points from neighbors. There is another serious problem in MGWR that it requires too much computing time and memory.
  3. In the results of HLM, there is only one estimate for \(\beta_1\) across the whole area. And estimates for \(\mu_1\), The problem lies in estimates for \(\gamma_1\) and \(\gamma_2\). As they are fixed effects in HLM, their estimates are also constant for all samples. However, spatial heterogeneity is expected in them.
  4. HGWR is the final solution. For global fixed effects, it generates globally constant estimates for all samples. For random effects, it would not smooth the estimates because they are not obtained by borrowing points. And for local fixed effects, we can discover spatial heterogeneity from their estimates. And it would not repeat computation for samples at each location. Thus, only the number of locations obviously affects the computation efficiency. This can reduce a large amount of computing time and memory.

There is an animation demonstrating the problem about bandwidth we addressed above.

As shown in this video, bandwidths have inequal spatial scale for two samples (represented by cubes). Both the samples represented by large red cubes and large blue cubes take 41 neighbour samples to calibrate GWR models. For the red one, neighbours on 8 nearest locations are taken. But the figure for the blue one is only 6. This situation means estimated coefficients are more smoothed for the red samples. In other words, estimations for the blue samples are much local.

HGWR overcome this drawback by introducing hierarchical structure with a special designed backfitting estimator. With the popularity of spatiotemporal big data, situations wherein the specific parameters for which HGWR was optimized are becoming more prevalent, suggesting that HGWR holds considerable promise as a useful tool for analyzing such data sets.

Estimation Errors

We can use some indicators to evaulate estimation errors for each model and coefficient. The following code generate a box-plot of absolute coefficient errors \(\mathrm{AE}\), which is \[ \mathrm{AE}_i = \left| r_i - e_i \right| \] where \(r_i\) reprsents the real value at sample \(i\), and \(e_i\) represents the corresponding estimate.

models_coef %>%
    map(~ select(.x, all_of(coef_names))) %>%
    map_dfr(function(x) {
        map2_dfr(x, names(x), ~ data.frame(ae = ae(beta0[[.y]], .x)), .id = "Coefficient")
    }, .id = "Algorithm") %>%
    mutate(Algorithm = ordered(as.factor(Algorithm), names(models_coef)),
           Coefficient = ordered(as.factor(Coefficient), coef_names)) %>%
    arrange(Coefficient, Algorithm) %>%
    ggplot(aes(x = Coefficient, y = ae, fill = Algorithm)) + geom_boxplot() +
        scale_y_log10(name = 'Squared Error', labels = ~ sprintf("%g", .x)) +
        scale_x_discrete(labels = coef_name_labels[coef_names]) +
        theme_bw() +
        theme(legend.position = "top", axis.text.y = element_text(angle = 90, hjust = 0.5))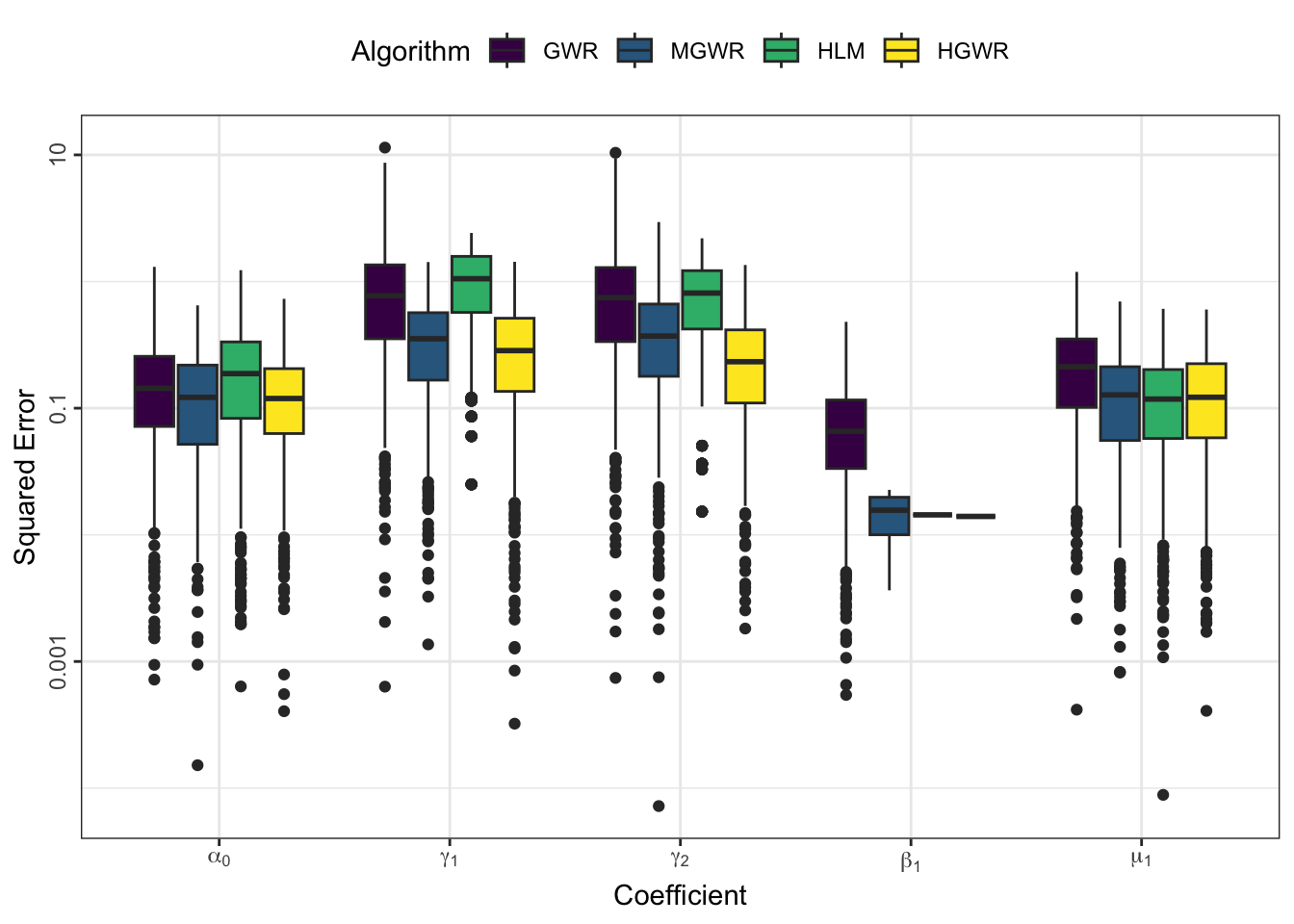

And the following code generate a bar-plot showing root mean squared errors \(\mathrm{RMSE}\) of each coefficient, which is \[ \mathrm{RMSE} = \sum_{i=1}^n \left(r_i-e_i\right)^2 \] where \(r_i\) reprsents the real value at sample \(i\), and \(e_i\) represents the corresponding estimate.

models_coef %>%
    map_dfr(function (alg) {
        map_dfr(coef_names, function (coef, real) {
            est_rmse <- rmse(real[[coef]], alg[[coef]])
            data.frame(Coefficient = coef, Value = est_rmse)
        }, beta0)
    }, .id = "Algorithm") %>%
    mutate(Algorithm = ordered(as.factor(Algorithm), c("GWR", "MGWR", "HLM", "HGWR")),
           Coefficient = ordered(as.factor(Coefficient), coef_names)) %>%
    ggplot(aes(x = Coefficient, y = Value, fill = Algorithm)) + 
        geom_bar(stat = 'identity', position = position_dodge()) + ylab("RMSE") +
        scale_y_continuous(limits = c(0, 1.6), oob = scales::squish, expand = expansion()) +
        scale_x_discrete(labels = coef_name_labels[coef_names]) +
        theme_bw() + theme(legend.position = "top")

From the perspective of estimation errors, HGWR significantly reduces the estimation error for local fixed effects. It can get over the affect of global fixed effects and random effects.

Summary

In this post we introduced how to calibrate an HGWR model using R package hgwrr. It is demonstrated that HGWR could properly estimate local fixed effects, global fixed effects, and random effects simultaneously. HGWR could usually successfully distinguish local fixed effects from other effect types. For local fixed effects, spatial heterogeneity is considered as with GWR; moreover, global fixed effects and random effects are estimated as accurately as when using HLM. Thus, HGWR can be regarded as a successful combination of GWR and HLM.

References

Brunsdon, Chris, A. Stewart Fotheringham, and Martin E. Charlton. 1996. “Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity.” Geographical Analysis 28 (4): 281–98. https://doi.org/10.1111/j.1538-4632.1996.tb00936.x.
Fotheringham, A. Stewart, Wenbai Yang, and Wei Kang. 2017. “Multiscale Geographically Weighted Regression (MGWR).” Annals of the American Association of Geographers 107 (6): 1247–65. https://doi.org/10.1080/24694452.2017.1352480.
Lu, Binbin, Chris Brunsdon, Martin Charlton, and Paul Harris. 2017. “Geographically Weighted Regression with Parameter-Specific Distance Metrics.” International Journal of Geographical Information Science 31 (5): 982–98. https://doi.org/10.1080/13658816.2016.1263731.
Raudenbush, Stephen W. 1993. “Hierarchical Linear Models and Experimental Design.” In Applied Analysis of Variance in Behavioral Science, 459–96. L. K. Edwards.